Khanh N. Dinh Lab
Associate Research Scientist in the Irving Institute for Cancer Dynamics and the Department of Statistics at Columbia University.

Office 601B
Schermerhorn Hall
Columbia University
1190 Amsterdam Avenue
New York, NY 10027
Our long-term research interests are in developing mathematical models and bioinformatic algorithms to characterize the formation and selection of biological processes during tumorigenesis. The methods are applicable to a wide range of cancer DNA-sequencing data, from bulk level down to the resolution of single cells, and help elucidating the evolutionary histories of mutations and different copy number aberration (CNA) mechanisms. Two major projects that we are working on are:
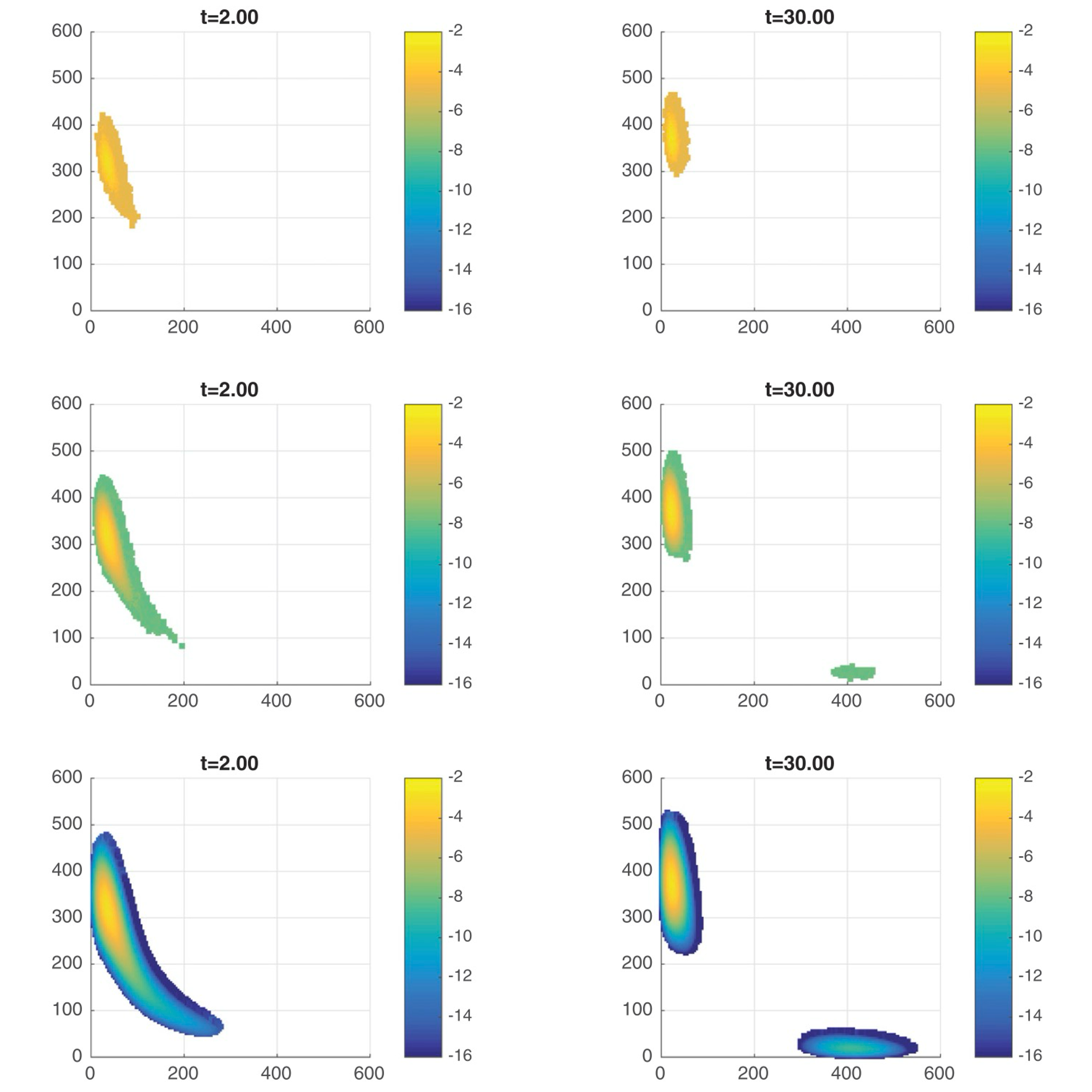
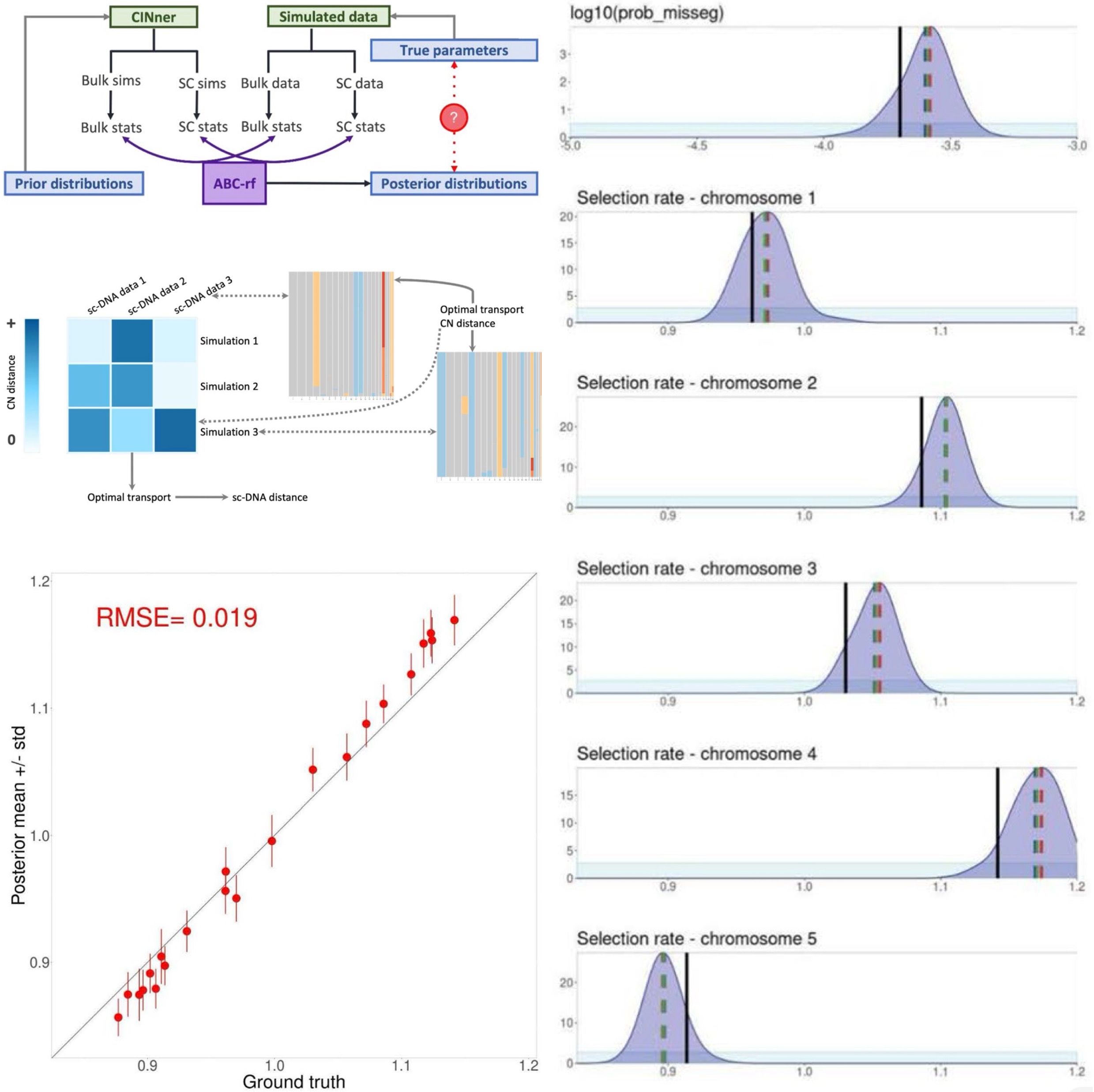
- Inference of chromosomal instability rates and selection coefficients of genomic regions in ovarian and breast cancers
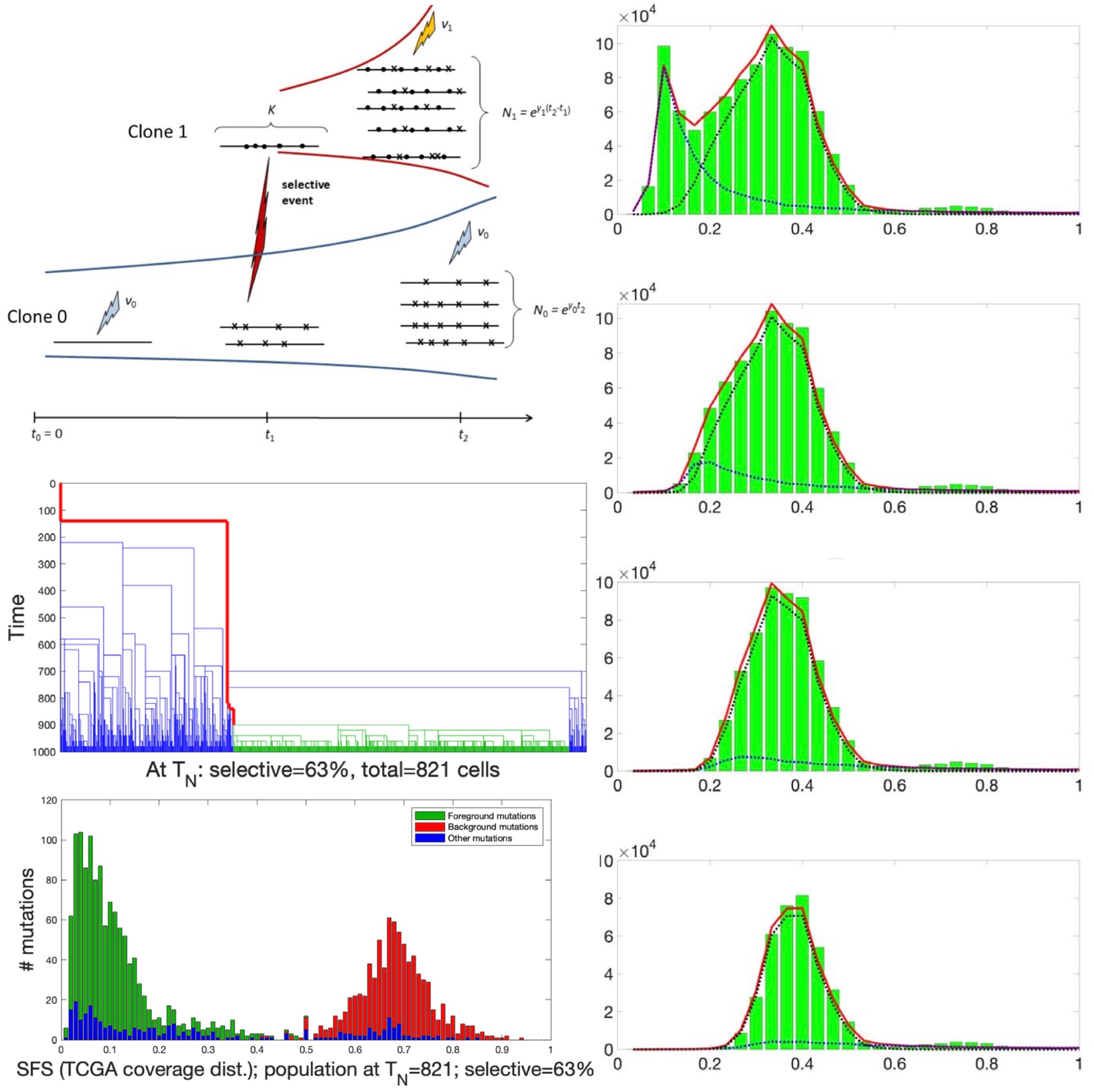
- Detection of clonality and estimation of clonal ages and growth rates from bulk DNA-sequencing data
news
| Nov 26, 2025 | Two of our works in 2025, which introduced algorithms CINner for simulating chromosomal instability and ABC-SMC-DRF for parameter inference, are included in IICD’s annual highlights. |
|---|---|
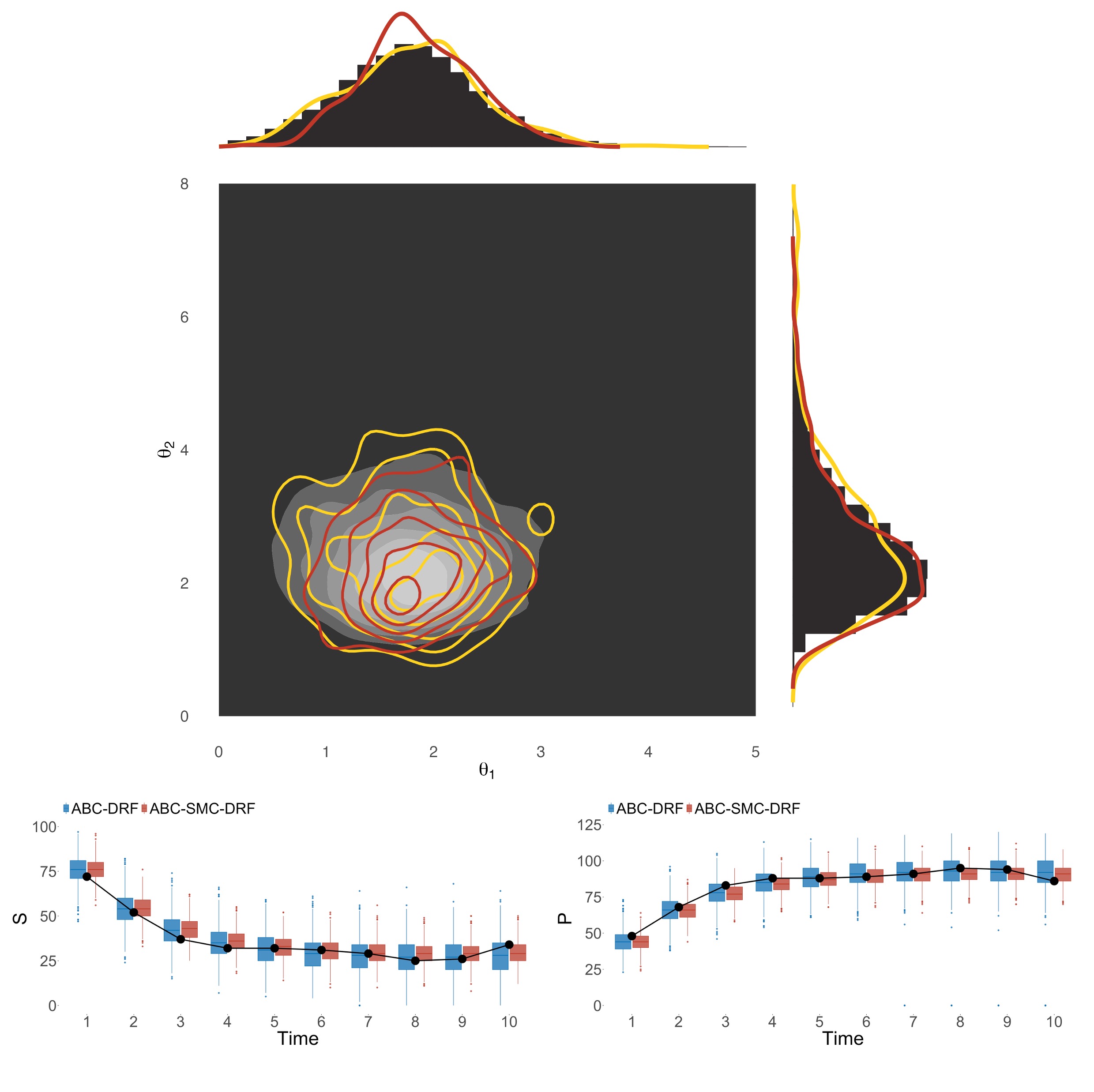
| Nov 05, 2025 | Our new paper introduces a novel noise-insensitive and efficient parameter inference algorithm. |
| Nov 04, 2025 | Our work on analyzing genomic, proteomic and metabolomic progression of bladder cancer at the whole-organ scale is highlighted on Nature Reviews Urology. |
| Jul 31, 2025 | We are showcased in a video featuring IICD at the Joint Statistical Meetings 2025. |
| Jul 28, 2025 | Sara El Baghdadi and Ethan Cohen, our 2025 Alliance interns, offer insights into their time in our Lab here. |
| Apr 04, 2025 | CINner, our computational framework for chromosomal instability, is published. |
| Feb 17, 2025 | Read the profile of Zijin Xiang, a former intern in our lab. |